839. Пересечение отрезков
Даны два отрезка на
плоскости с целочисленными координатами их концов в декартовой системе
координат. Определите, имеют ли отрезки общую точку.
Вход. В первой строке заданы координаты первого конца первого
отрезка, во второй строке – второго конца первого отрезка. В третьей и
четвёртой строках заданы координаты концов второго отрезка. Все координаты
являются целыми числами, по модулю не превышающими 104.
Выход. Выведите “Yes”, если отрезки
имеют общую точку, и “No” в противном случае.
|
Пример
входа 1 |
Пример
выхода 1 |
|
0 0 1 0 1 0 1 1 |
Yes |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
0 0 1 0 2 0 3 0 |
No |
РЕШЕНИЕ
геометрия
Анализ алгоритма
Ограничивающий прямоугольник геометрической фигуры – это наименьший прямоугольник,
стороны которого параллельны осям координат, и который полностью содержит
данную фигуру.
Проще говоря, если мы хотим “вписать”
фигуру в прямоугольник так, чтобы все её точки были внутри, ограничивающий
прямоугольник будет минимального размера.
Рассмотрим отрезок с концами в
точках (x1, y1)
и (x2, y2). Чтобы найти его ограничивающий
прямоугольник:
·
Определим
левый нижний угол прямоугольника:
x1’ = min(x1,
x2), y1’ = min(y1, y2)
·
Определим
правый верхний угол прямоугольника:
x2’ = max(x1,
x2), y2’ = max(y1, y2)
Таким образом, ограничивающий
прямоугольник — это прямоугольник с углами (x1’, y1’) и (x2’,
y2’), который содержит наш отрезок.

Лемма. Пусть на прямой заданы два
отрезка (x1, x2) и (x3, x4), где x1 < x2 и x3 < x4. Отрезки не пересекаются тогда и только тогда, когда либо первый отрезок расположен левее второго, либо
второй расположен левее первого.
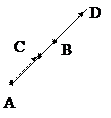
Лемма. Пусть на плоскости заданы два прямоугольника
(x1, y1) – (x2, y2) и (x3, y3) – (x4, y4), где
x1 < x2, y1 < y2 и x3 < x4, y3 < y4. Прямоугольники
не пересекаются тогда и только
тогда, когда либо не пересекаются отрезки (x1, x2) и (x3, x4), либо не пересекаются отрезки (y1, y2) и (y3, y4).

Критерий пересечения двух
отрезков
Два отрезка AB и CD пересекаются тогда и только тогда, когда выполняются три условия:
1. Ограничивающие прямоугольники
пересекаются.
2. Точки C и D находятся
по разные стороны от прямой AB или хотя бы одна точка C или D
лежит на прямой AB. Это значит, что
[AB ? AC] * [AB ? AD] ? 0
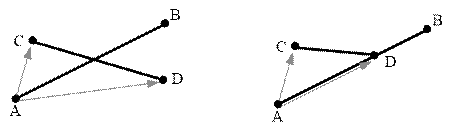
3. Точки A и B находятся
по разные стороны от прямой CD или хотя бы одна точка A или B
лежит на прямой CD. Это значит, что
[CD ? CA] * [CD ? CB] ? 0

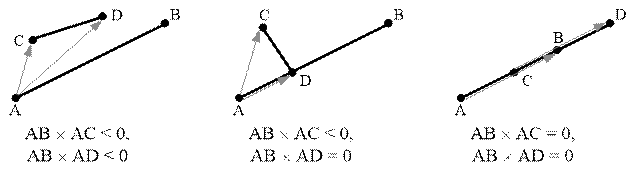
Ниже приведены различные
случаи взаимного расположения двух отрезков и соответствующие им значения
векторных произведений.
В следующем примере каждый из отрезков пересекает прямую, содержащую
другой отрезок. Однако ограничивающие их прямоугольники не пересекаются.
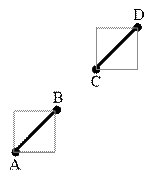
Пример
В первом примере отрезки пересекаются. Во втором примере
– нет.
Реализация алгоритма
Поскольку координаты концов отрезков являются целыми числами, при
вычислениях мы будем использовать только целочисленный тип long long.
В дальнейшем нам понадобится функция sgn, определяющая знак числа
n.
int sgn(long
long n)
{
return (n
> 0) - (n < 0);
}
Функция RectanglesIntersects принимает в качестве
аргументов координаты ограничивающих прямоугольников для отрезков AB и CD. Она
позвращает 1, если прямоугольники (x1, y1) – (x2, y2) и (x3, y3) – (x4, y4) пересекаются, и 0 в
противном случае.
int RectanglesIntersect(long long x1, long long y1,
long long x2, long long y2,
long long x3, long long y3,
long long x4, long long y4)
{
if (x2 < x3 || x4 < x1) return 0;
if (y2 < y3 || y4 < y1) return 0;
return 1;
}
Функция cross вычисляет векторное
произведение двух векторов (Ax, Ay)
и (Bx, By).
long long
cross(long long Ax, long long Ay,
long long Bx, long long By)
{
return Ax * By - Ay * Bx;
}
Функция intersect проверяет, пересекаются ли отрезки AB и CD.
int segmentsIntersect(long long x1, long long y1,
long long x2, long long y2,
long long x3, long long y3,
long long x4, long long y4)
{
Проверяем пересечение ограничивающих
прямоугольников. Если они не пересекаются, то возвращаем 0.
if (!RectanglesIntersect(
min(x1, x2), min(y1, y2), max(x1, x2), max(y1, y2),
min(x3, x4), min(y3, y4), max(x3, x4), max(y3, y4))
) return 0;
Строим вектора AB, AC, AD.
long long ABx = x2 - x1, ABy = y2 - y1;
long long ACx = x3 - x1, ACy = y3 - y1;
long long ADx = x4 - x1, ADy = y4 - y1;
Строим вектора CD, CA, CB.
long long CDx = x4 - x3, CDy = y4 - y3;
long long CAx = x1 - x3, CAy = y1 - y3;
long long CBx = x2 - x3, CBy = y2 - y3;
Вычисляем векторные произведения.
long long ABxAC = cross(ABx, ABy, ACx, ACy); // AB x AC
long long ABxAD = cross(ABx, ABy, ADx, ADy); // AB x AD
long long CDxCA = cross(CDx, CDy, CAx, CAy); // CD x CA
long long CDxCB = cross(CDx, CDy, CBx, CBy); // CD x CB
Прорверяем пункты 2 и 3 критерия
пересечения отрезков. Если они не выполняются, то возвращаем 0. Чтобы
избежать переполнения, следует сравнивать с нулем не произведение чисел, а произведение их знаков.
if (sgn(ABxAC) * sgn(ABxAD)
> 0) return 0;
if (sgn(CDxCA) * sgn(CDxCB)
> 0) return 0;
return 1; // Отрезки пересекаются
}
Основная часть
программы.
Читаем входные данные.
scanf("%lld %lld %lld %lld",&x1,&y1,&x2,&y2);
scanf("%lld %lld %lld %lld",&x3,&y3,&x4,&y4);
Проверяем пересечение отрезков.
if (segmentsIntersect(x1, y1, x2, y2, x3, y3, x4, y4))
puts("Yes");
else
puts("No");